Oompa, Loompa, doompa-dee-do
I’ve got a perfect puzzle for you
Remember the disastrous “Willy Wonka Experience” in Glasgow a few weeks ago? Parents paid £35 per ticket, lured in by AI-generated ads depicting a lush candy paradise only to be greeted by a near-empty warehouse with a couple dinky decorations. Now nobody trusts Willy Wonka. Perhaps we never should have. After all, this is the man who invited five children to his factory and set them up to meet grisly fates.
This week Wonka will expose you for the conman you are. Wait a minute. Strike that. Reverse it.
Did you miss last week’s puzzle? Check it out here, and find its solution at the bottom of today’s article. Be careful not to read too far ahead if you haven’t solved last week’s yet!
Puzzle #34: Fool’s Golden Ticket
Willy Wonka is selling new chocolate bars. They’re rectangular bars comprised of a 3×7 array of individually filled chocolate squares. Some squares are filled with fizzy lifting drink, while others have snozzberry filling. The arrangement of the flavors is randomly assigned from bar to bar.
Notice in the bar above that the four squares marked 1 form a rectangle whose corners are all snozzberry, whereas the squares marked 2 form a rectangle whose corners are all fizzy lifting drink (two-by-twos and three-by-threes are still rectangles). Wonka promises that anybody who buys a bar where NO four squares of the same type form a rectangle will win a visit to his factory. Your Uncle Joe starts emptying your life savings for chocolate, but you sense a scam. How can you convince Uncle Joe that Wonka’s winning bars don’t exist?
I’ll be back next Monday with the answer and a new puzzle. Do you know a cool puzzle that you think should be featured here? Message me on X @JackPMurtagh or email me at gizmodopuzzle@gmail.com
Solution to puzzle #33: Pi Day
Did you run circles around last week’s puzzles? Shout-out to reiderrabbitt111 for solving them both.
A string is tightly wrapped around Earth’s equator. You splice additional string in to add just enough slack so that you could (in principle) raise the new longer string exactly one foot off the ground all around the world. How much string did you add? How much would you need to add to a string wrapped around a basketball to raise it by one foot?
You would need to add 2π or about 6.283 feet of string in both cases.
There are two things I find amazing about this solution. One is that 6 feet of string is tiny compared to the circumference of the Earth, and I’m surprised it results in so much slack to distribute around the globe. The other is that the answer does not depend at all on the size of the sphere. A marble, a basketball, and the Earth all need the same adjustment.
To solve this, recall that a circle with radius r has a circumference of 2πr. The question at the heart of this puzzle is: how much longer does the circumference become when the radius grows by one foot? The circumference of the longer string is 2π(r+1). The difference in lengths between the longer string and the original string is then 2π(r+1) – 2πr = 2π.
The second puzzle asked whether the yellow, blue, or red area in the image below is the largest:

In fact all three areas are the same! You could solve this by comparing the radii of the circles to the side length of the squares in each case, but there’s a perspective I like even more.
Whenever you inscribe a single circle inside of a square, the area of the circle is always exactly π/4 or 78.5% of the area of the square. To see this, suppose the circle has radius r and note that the square then has side length 2r and thus area 4r². Dividing the area of the circle (πr²) by the area of the square gives π/4. Again, the radii cancel and we’re left with a number that’s independent of the sizes of the shapes.
We can imagine the blue square broken into four smaller squares, each of which has an inscribed circle like below.
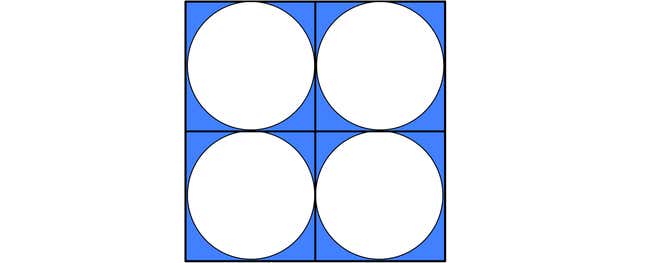
The circles take up about 78.5% of the area in each of the small squares and therefore also take up 78.5% of the area of the big square. The same argument goes for all three colors. Since the big squares are all the same sizes, the three colored regions all have the same area.
Leave A Comment
You must be logged in to post a comment.